Tétracorde

Le tétracorde est le nom donné à une succession de quatre notes conjointes comme do re mi fa, qui forment un intervalle dit de quarte juste [2 tons et un demi ton]. Le tétracorde est un concept central dans les théories astronomiques-mathématiques de la grèce antique qui ont été héritées par l'âge d'or de la civilisation arabe, puis par le Moyen-Âge occidental. C'est à partir du tétracorde qu'on calcule les intervalles des échelles (gammes) musicales (comment se répartissent les intervalles au sein de la quarte juste), mais aussi la composition des modes, qui comportent deux tétracordes. La gamme majeure est construite avec deux tétracordes identiques séparés par un ton :

1er tétracorde : I. (do) + 1 ton II. (re) + 1 ton III. (mi) + 1/2 ton IV. (fa)

+ 1 ton

2e tétracorde : V. (sol) + 1 ton VI. (la) + 1 ton VII. (si) + 1/2 ton I. (do)

On remarque que cette symétrie entraîne que le premier tétracorde de do (do, re, mi, fa, sol) et aussi le second tétracorde de la gamme de fa majeur (fa, sol, la, si, do, re, mi, fa) et que le second est le premier de la gamme de sol majeur (sol, la, si, do, ré, mi, fa♯, sol). C'est à dire que les tonalités dites proches se chevauchent par leurs tétracordes.

Bibliographie

Barbera C. André. Arithmetic and Geometric Division of the Tetrachord. Journal of Music Theory, (21) 1977 p. 294-323

Document

Jean-Jacques Rousseau, Dictionnaire de musique, 1764 (2) p. 134-138.

TÉTRACORDE, s. m. C'étoit, dans la musique ancienne, un ordre ou système particulier de sons dont les cordes extrêmes sonnoient la quarte : ce système s'appeloit tétracorde, parce que les sons qui le composoient étoient ordinairement au nombre de quatre ; ce qui pourtant n'étoit pas toujours vrai.

Nicomaque, au rapport de Boëce, dit que la musique, dans sa première simplicité, n'avoit que quatre sons, ou cordes, dont les deux extrêmes sonnoient le diapason entre elles, tandis que les deux moyennes, distantes d'un ton l'une de l'autre, sonnoient chacune la quarte avec l'extrême dont elle étoit le plus proche, et la quinte avec celle dont elle était le plus éloignée; il appelle cela le tétracorde de Mercure, du nom de celui qu'on en disoit l'inventeur.

Boëce dit encore qu'après l'addition de trois cordes faite par différens auteurs, Lychaon, Samien, en ajouta une huitième, qu'il plaça entre la trite et la paramèse, qui étoient auparavant la même corde ; ce qui rendit l'octacorde complet et composé de deux tétracordes disjoints, de conjoints qu'ils étoient auparavant dans l'eptacorde.

J'ai consulté l'ouvrage de Nicomaque, et il me semble qu'il ne dit point cela ; il dit au contraire que Pythagore ayant remarqué que, bien que le son moyen des deux tétracordes conjoints sonnât la consonnance de la quarte avec chacun des extrêmes, ces extrêmes comparés entre eux étoient toutefois dissonants, il inséra entre les deux tétracordes une huitième corde, qui, les divisant par un ton d'intervalle, substitua le diapason ou l'octave à la septième entre leurs. extrêmes, et produisit encore une nouvelle consonnance entre chacune des deux cordes moyennes et l'extrême qui lui étoit opposée.

Sur la manière dont se fit cette addition, Nicomaque et Boëce sont tous deux également embrouillés; et, non contens de se contredire entre eux, chacun d'eux se contredit encore lui-même. (Voyez SYSTÈME, TRITE, PARA MÈSE. )

Si l'on avoit égard à ce que disent Boëce et d'autres plus anciens écrivains, on ne pourroit donner de bornes fixes à l'étendue du tétracorde ; mais, soit que l'on compte ou que l'on pèse les voix, on trouvera que la définition la plus exacte est celle du vieux Bacchus, et c'est aussi celle que j'ai préférée.

En effet, cet intervalle de quarte est essentiel au tétracorde ; c'est pourquoi les sons extrêmes qui forment cet intervalle sont appelés immuables ou fixes par les anciens, au lieu qu'ils appellent mobiles ou changeants les sons moyens, parce qu'ils peuvent s'accorder de plusieurs manières.

Au contraire, le nombre de quatre cordes, d'où le tétracorde a pris son nom, lui est si peu essentiel, qu'on voit, dans l'ancienne musique, des tétracordes qui n'en avoient que trois; tels furent, durant un temps, les tétracordes enharmoniques ; tel étoit, selon Meibomius, le second tétracorde du système ancien avant qu'on y eût inséré une nouvelle corde.

Quant au premier tetracorde, il étoit certainement com plet avant Pythagore, ainsi qu'on le voit dans le pythagoricien Nicomaque ; ce qui n'empêche pas M. Rameau d'affirmer que, selon le rapport unanime, Pythagore trouva le ton, le diton, le semi-ton, et que du tout il forma le tétracorde diatonique (notez que cela feroit un pentacorde) : au lieu de dire que Pythagore trouva seulement les raisons de ces intervalles, lesquels, selon un rapport plus unanime, étoient connus longtemps avant lui.

Les tétracordes ne restèrent pas long-temps bornés au nombre de deux; il s'en forma bientôt un troisième, puis un quatrième, nombre auquel le système des Grecs demeura fixé.

Tous ces tétracordes étoient conjoints, c'est-à-dire que la dernière corde du premier servoit toujours de première corde au second, et ainsi de suite, excepté un seul lieu à l'aigu ou au grave du troisième tétracorde, où il y avoit disjonction, laquelle (voyez ce mot) mettoit un ton d'intervalle entre la plus haute corde du tétracorde inférieur et la plus basse du tétracorde supérieur. (Voyez SYNAPHE, DIAZEUXIS.) Or, comme cette disjonction du troisième tétracorde se faisoit tantôt avcc le second, tantôt avec le quatrième, cela fit approprier à ce troisième tétracorde un nom particulier pour chacun de ces deux cas; de sorte que, quoiqu'il n'y eût proprement que quatre tétracordes, il y avoit pourtant cinq dénominations. (Voyez planche 13.)

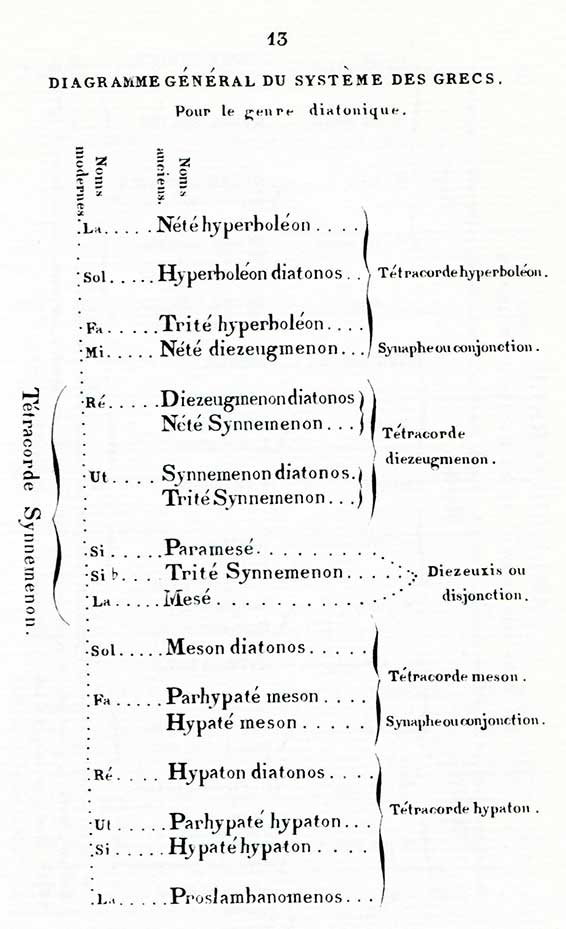
Voici les noms de ces tétracordes : le plus grave des quatre, et qui se trouvoit placé un ton au dessus de la corde proslambanomène, s'appeloit le tétracorde hypaton, ou des principales ; le second en montant, lequel étoit toujours conjoint au premier, s'appeloit le tétracorde méson, ou des moyennes ; le troisième, quand il étoit conjoint au second et séparé du quatrième, s'appeloit le tétracorde synnéménon, ou des conjointes ; mais quand il étoit séparé du second et conjoint au quatrième, alors ce troisième tétracorde prenoit le nom de diézeugménon, ou des divisées ; enfin le quatrième s'appeloit le tétracorde hyperboléon, ou des excellentes. L'Arétin ajouta à ce système un cinquième tétracorde, que Meibomius prétend qu'il ne fit que rétablir. Quoi qu'il en soit, les systèmes particuliers des tétracordes firent enfin place à celui de l'octave, qui les fournit tous.

Les deux cordes extrêmes de chacun de ces tétracordes étoient appelées immuables, parce que leur accord ne changeoit jamais; mais ils contenoient aussi chacun deux cordes moyennes, qui, bien qu'accordées semblablement dans tous les tétracordes, étoient pourtant sujettes, comme je l'ai dit, à être haussées ou baissées selon le genre, et même selon l'espèce du genre, ce qui se faisoit dans tous les tétracordes également; c'est pour cela que ces cordes étoient appelées mobiles.

Il y avoit six espèces principales d'accords, selon les aristoxéniens ; savoir, deux pour le genre diatonique, trois pour le chromatique, et une seulement pour l'enharmonique. ( Voyez ces mots. ) Ptolomée réduit ces six espèces à cinq. ( Voyez planche 23, figure I.)

Ces diverses espèces, ramenées à la pratique la plus commune, n'en formoient que trois, une par genre.

I. L'accord diatonique ordinaire du trétracorde formoit trois intervalles, dont le premier étoit toujours d'un semi-ton, et les deux autres d'un ton chacun, de cette manière, mi, fa, sol, la.

Pour le genre chromatique, il falloit baisser d'un semi- ton la troisième corde, et l'on avoit deux semi-tons consécutifs, puis une tierce mineure, mi, fa, fa dièse, la.

Enfin, pour le genre enharmonique, il falloit baisser les deux cordes du milieu jusqu'à ce qu'on eût deux quarts-de-ton consécutifs, puis une tierce majeure, mi, mi demi- dièse, fa, la ; ce qui donnoit entre le mi dièse et le fa un véritable intervalle enharmonique.

Les cordes semblables, quoiqu'elles se solfiassent par les mêmes syllabes, ne portoient pas les mêmes noms dans tous les tétracordes; mais elles avoient dans les tétracordes graves des dénominations différentes de celles qu'elles avoient dans les tétracordes aigus. On trouvera toutes ces différentes dénominations dans la planche 13.

Les cordes homologues, considérées comme telles, portoient des noms génériques qui exprimoient le rapport de leur position dans leurs tétracordes respectifs: ainsi l'on donnoit le nom de barypycni aux premiers sons de l'intervalle serré, c'est-à-dire au son le plus grave de chaque tétracorde; de mesopycni aux seconds ou moyens; d'oxypycni aux troisièmes ou aigus; et d'apycni à ceux qui ne touchoient d'aucun côté aux intervalles serrés. (Voyez SYSTÈME. )

Cette division du système des Grecs par tétracordes semblables, comme nous, divisons le nôtre par octaves semblablement divisées, prouve, ce me semble, que ce système n'avoit été produit par aucun sentiment d'harmonie, mais qu'ils avoient tâché d'y rendre par des intervalles plus serrés les inflexions de voix que leur langue sonore et harmonieuse donnoit à leur récitation soutenue, et surtout à celle de leur poésie, qui d'abord fut un véritable chant; de sorte que la musique n'étoit alors que l'accent de la parole, et ne devint un art séparé qu'après un long trait de temps. Quoi qu'il en soit, il est certain qu'ils bornoient leurs divisions primitives à quatre cordes, dont toutes les autres n'étoient que les répliques, et qu'ils ne regardaient tous les autres tétracordes que comme autant de répétitions du premier.

D'où je conclus qu'il n'y a pas plus d'analogie entre leur système et le nôtre qu'entre un tétracorde et une octave, et que la marche fondamentale à notre mode, que nous donnons pour base à leur système, ne s'y rapporte en aucune façon :

1° Parce qu'un tétracorde formoit pour eux un tout aussi complet que le forme pour nous une octave ;

2° Parce qu'ils n'avoient que quatre syllabes pour solner, au lieu que nous en avons sept ;

3° Parce que leurs tétracordes étoient conjoints ou disjoints à volonté: ce qui marquoit leur entière indépendance respective ;

4° Enfin, parce que les divisions y étoient exactement semblables dans chaque genre, et se pratiquoient dans le même mode ; ce qui ne lpouvoit se faire dans nos idées par aucune modulation véritablement harmonique.

Planche 13

Musicologie.org 2008