Nicomaque de Gérase : « Fragments relatifs à l'Harmonique »

Premier fragment¹

9. On rapporte que Hermès inventa la lyre cconstruite avec la tortue et qu'après l'avoir munie de sept cordes, il transmit l'art d'en jouer à Orphée. Orphée à son tour l'enseigna à Thamyris et à Linus, puis Linus à Hercule, de la main duquel il périt. Il l'enseigna aussi au Tbében Amphion qui bâtit la ville de Thèbes et fui donna sept poroles en considération des sept cordes. Orphée mis à mort par les femmes de Thrace, sa lyre fut, dit-on, jetée à la mer qui la rejeta sur la côte près la, ville d'Antissa, dans Lesbos. On ajoute que des pêcheurs qui l'avaient trouvée la portèrent à Terpandre et qhe celui-ci l'emporta en Égypte qu'après l'avoir travaillée avec grand soin, il la fit voir aux prètres égyptiens et se donna comme en étant le premier inventeur. C'est dans ce sens que l'on dit Terpandre inventeur de la lyre ; mais des anciens² prétendent qu'elle doit son origine à Cadmus, fils d'Agérior.

1. L'ensemble de ces fragments constitue dans les manuscrits et les éditions le prétendu livre II du Manuel d'harmonique.

2. Vulgate, ἀχαίους. Meursius propose ἀρχαίους, leçon adoptée par Meybaum et, sous toutes réserves, par le traducteur.

II^e fragment

1. Voici les nombres avec lesquels les musiciens forment les intervalles d'un ton.

2. Pour la quarte, que l'on dit considérer suivant le rapport sesquitiers et qui se compose de deux tons et d'une certaine fraction, par exemple l'intervalle commençant avec l'hypate des hypates et se terminant sur l'hypate des moyennes, on prend comme nombre¹ sesquitiers le nombre 256 qui l'est de 192, et partant de ce nombre de 192, en passant par les rapports sesquioctaves suivant lesquels on considère les intervalles toniés, ils complètent le nombre 216. On surtend donc un ton à partir de 192 et l'on produit 216 qui est le sesquioctave de 192, car il contient 192 plus son 8^e, 24. Puis, à partir de 216, on surtend encore un ton et l'on produit 243, sesquioctave de 216, car il contient ce nombre plus son 8e, 27. Maintenant, pour compléter la quarte et le nombre 256, il manque 13, ce qui n'est la moitié ni du premier ton, considéré dans le nombre 24, ni du second, considéré dans le nombre 27.

3. Pour la quinte, qui réside dans le rapport sesquialtère, et se compose de trois tons et d'une certaine fraction, par exemple l'intervalle commençant avec la parhypate des moyennes et se terminant sur la trite des disjointes, on opère de la manière suivante. On prend un nombre sesquialtère, soit 768, qui l'est de 512, puis, passant par les sesquioctaves, suivant lesquels on considère les intervalles toniés et par le limma ou reste, on complète le nombre 768. Partant donc du nombre 512, on surtend un ton et l'on produit le nombre 576, qui est sesquioctave de 512, car il contient le nombre 512 lui-même, plus son 8^e, 64. A partir de 576, on surtend encore un ton et l'on produit son sesquioctave 648, qui est bien sesquioctave de 576, puisqu'il contient ce nombre plus son 8^e, 72. A partir de 648, on surtend encore un ton et l'on produit son sesquioctave 729, qui est bien son sesquioctave, puisqu'il le surpasse de 81, qui est le 8^e de 648. Maintenant, pour compléter le nombre sesquialtère 768, il manque 39 ; or ce nombre n'est la moitié ni de 64, suivant lequel on a considéré le premier ton, ni de 72, rapporté au deuxième ton, ni de 81, rapporté au troisième, car le ton ne se divise pas exactement en deux demi-tons.

4. Maintenant, pour la quarte, qui se compose d'un ton, d'un limma et d'un ton, telle que celle qui commence avec le proslambanomène et se termine sur la diatonique des hypates, on opère ainsi. On prend un nombre sesquitiers, 288, qui l'est de 216, et, à partir de 216, on surtend un ton et l'on produit 243, sesquioctave de 216 et le surpassant de 27. Mais, comme nous ne pouvons plus surtendre un ton à partir de 243² car nous trouvons que cette corde³ ne réalise pas un sesquioctave, nous produisons par relâchement un ton sous-sesquioctave de 288 ; or le sous-sesquioctave de 288 est 256, puisque celui-ci est contenu en entier dans 288, ainsi que son 8^e, 32⁴. Ainsi donc, par suite de la surtension opérée à partir de 216, suivant le rapport sesquioctave du ton, on trouvait 243, et, par le relâchement d'un ton, 256 ; mais, pour compléter le nombre intermédiaire, il manque 13, ce qui n'est la moitié ni de 27 ni de 32. D'autre part, le système total de la quarte, quant aux nombres précités, est de 72⁵ ; dans le nombre sesquioctave obtenu par surtension, on trouvera 27, et dans celui qu'on aura obtenu par relâchement, 32 ; or, si de 72 nous retranchons 27 et 32, il nous reste 13, qui n'est la moitié ni de 27 ni de 32.

5. Pour la quinte, qui se compose d'un ton, d'un limma et de deux tons, telle que celle qui commence avec la diatonique des hypates et se termine sur la mèse, on opère ainsi. On prend un nombre sesquialtère, tel que 1296 qui l'est de 864, et, partant de ce nombre, on surtend un ton et l'on produit le nombre 972 qui surpasse de 108 le nombre 864 ; mais, comme nous ne pouvons plus surtendre un ton à partir de 972⁶, nous trouvons aussi (le nombre voulu) par relâchement. Nous relâchons donc, à partir de 1296, 1152, qu'il surpasse du nombre 144, qui est le 8^e de 1152. Nous relâchons encore un ton à partir de 1152 et nous trouvons 1024, nombre sous-sesquioctave⁷ de 1152 et surpassé par lui de 128, qui est le 8^e de 1024. Ainsi donc, de 1024 retranchons 972, nombre où réside le ton obtenu par surtension à partir de 864 : reste 52, sans que l'on puisse trouver aucun nombre, parmi les tons, dont celui-ci, 52, soit la moitié ; car il ne l'est ni de 108, ni de 128, ni de 144, nombres auxquels correspondaient les intervalles toniés que l'on a trouvés tout à l'heure.

Notes

1. Il faudrait rapport (λόγος), mais nous avons déjà vu cette substitution de termes (ci-dessus, p. 23, note 3).

2. En effet, l'intervalle placé ici dans la donnée est le limma et non pas le ton.

3. Vulgate, αὐτήν, pas de variante connue. Meybaum propose αὐτόν, mais αὐτήν peut se soutenir et doit peut-être être conservé, car l'impossibilité de réaliser un ton après l'hypate des hypates existe aussi bien pour cette corde (αὐτήν) que pour le nombre (αὐτόν) qui lui correspond.

4. Pour trouver le sous-sesquioctave d'un nombre, on divise ce nombre par 9 et l'on soustrait le quotient. Ex. : 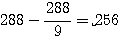. Par contre, .

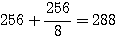5. En effet, 72 est la différence de 288 à 216, nombres correspondants, d'après la donnée, aux deux limites de cette quarte.

6. En effet, le second intervalle, dans la donnée, est un demi-ton et non pas un ton.

7. Vulgate, ἐπόγδοον. Il faut ὑπεπόγδοον, comme Meybaum l'a remarqué.

III^e fragment

1. Extrait¹ — Suivant le dire de Nicomaque², on a nommé hypate la corde la plus haute et la première, parmi les divisions de la lyre à sept sons³, parce que Cronos (Saturne) est (l'astre) le plus élevé et le premier à partir de la sphère fixe. La nète a été rapportée à la Lune comme étant la dernière des autres sphères⁴, — la mèse au Soleil, — les cordes placées de chaque côté de la nète et de l'hypate, savoir, la parhypate à Zeus (Jupiter), et la paranète, non pas à Hermès (Mercure), mais, irrégulièrement, à Aphrodite (Vénus), à moins qu'il n'y ait une faute dans le texte, — l'hypermèse⁵ à Arès (Mars), — la trite à Aphrodite⁶. La sphère aiguë est la Lune qui a le même rapport que la nète ; la sphère grave est Saturne, puisqu'elle a le même rapport que l'hypate.

2. Ceux qui font commencer (la série planétaire) par les astres voisins de nous, disent que l'hypate correspond au premier astre, la Lune, comme point de départ des sons; que la nète est la corde de Saturne, vu que celui-ci est le plus éloigné de nous. En effet, l'hypate a plus d'affinités avec les êtres engendrés, en raison de ce que dans une essence multiple la puissance est plus faible, de sorte que par ce qu'elle a de terrestre elle est multiple, et par ce qu'elle a de multiple elle est faible; car c'est surtout dans le fait d'être un que consiste la puissance. D'après cela, l'hypate a été rapportée à la Lune, comme étant une sphère de forme variée et d'un mouvement multiple, ne possédant pas une aussi grande puissance à cause de son éloignement des premières, et aussi parce qu'il y a comme une station pour les corps célestes quand on arrive à celui-ci⁷, de même que pour les sons qui partent de la nète, quand ils arrivent à l'hypate, sans admettre une nature de semblable essence pour les corps placés par devant⁸. Voilà comment cette corde a été attribuée à la Lune.

3. En effet, la première (planète) que nous rencontrons est la Lune, puisque c'est la plus proche de la Terre; et le son grave sort des cavités qui environnent les flancs, qui sont les parties inférieures du corps humain, tandis que le son aigu part des oreilles et des parties supérieures⁹.

4. Par conséquent la nète est la corde de Saturne, vu que cette planète n'est pas apte à recevoir une augmentation¹⁰ et qu'elle renferme toutes les autres et en essence et en puissance. Ainsi donc, si l'une (la Lune) est lente et l'autre (Saturne) rapide, quant au mouvement de translation des planètes dans l'univers, à ces divers points de vue et au point de vue de l'éloignement¹¹, la Lune est bien l'hypate. En effet Saturne est beaucoup plus proche de la sphère fixe, dont il n'est éloigné que d'un 30e de degré, de sorte que, dans un mouvement égal, il ne dévie de la révolution totale de l'Univers que de 2 minutes diurnes, ce qui est le 30e d'un degré; or, si l'on examine la Lune dans son mouvement égal et moyen, on pourra reconnaître qu'elle est éloignée de 13 à 14 degrés (de la sphère fixe), de sorte qu'il y a lieu d'établir que celui-ci (Saturne) est la plus rapide de toutes (les planètes) et que la Lune en est la plus lente.

Notes

1. Nous traduisons ainsi le mot ὅτι placé ici, comme dans la plupart des recueils d'Excerpta, notamment dans la Bibliothèque de Photius. Ce mot indique, le plus souvent, une citation textuelle.

2. Cf. ci-dessus, Manuel d'harmonique, ch. iii. — Ce troisième fragment a été reproduit presque textuellement par Manuel Bryenne (Harmoniques, l. II, section v), éd. unique de Wallis, p. 410-413.

3. Texte altéré. Lire peut-être ὡς τῶν ἐν ἐπραφθ. διαιρ. Cf. Bryenne, Harmoniques, éd. unique de Wallis, p. 365.

4. Les sphères errantes, les planètes.

5. Vulgate, παραμέσην. Correction de Meybaum.

6. Il faudrait : la paramèse à Hermès.

7. En d'autres termes, la Lune est sur une ligne qui, partant des étoiles fixes, aboutirait à la Terre, le dernier astre doué de mouvement.

8. La Terre, par exemple, considérée ici comme immobile.

9. Cf. Cl. Ptolémée, Harmoniques, l. III, ch. x.

10. C'est-à-dire, probablement, qu'après Saturne on ne peut supposer l'addition d'une planète plus éloignée de la terre.

11. Nous lisons comme Meybaum, d'après Bryenne, κατὰ ταῦτα et κατ' ἀπόλειψιν.

IV^e fragment

1. Extrait. — Tous ceux qui ont adjoint d'autres cordes à la huitième ont été guidés, non point par une raison quelconque, mais par le désir de gagner l'âme de leurs auditeurs. C'est ainsi que la neuvième corde fut ajoutée par Théophraste de Piérie, la dixième par Histiée de Colophon, la onzième par Timothée de Milet, et les suivantes par d'autres encore.

2. Plus tard, le nombre des cordes fut porté à dix- huit. Aussi voit-on Phérécrate, le poète comique, dans sa pièce intitulée Chiron, faire un reproche à ces novateurs du laisser-aller qui régnait dans leurs mélodies¹.

3. Les cordes sont en tout, dans les trois genres, au nombre de vingt-huit. Il n'y en a ni plus ni moins, car la voix humaine ne peut admettre, ni, dans le grave, des sons plus graves, sans arriver au son de la trompe et au bruit de la toux; sons insignifiants, inarticulés et non mélodieux; — ni, dans l'aigu, les sons qui ressemblent aux mugissements des bœufs ou aux hurlements du loup, lesquels sont inappréciables, discordants, et ne peuvent participer à une consonance².

4. Les cordes comprises dans chaque (genre), d'après le système de ceux qui font deux mèses dans les tétracordes disjoints, de manière qu'un tétracorde soit consonnant par disjonction à un pentacorde³, sont au nombre de 18 ; tandis que ceux qui ne font pas plus d'une mèse dans le système immuable⁴, mais l'emploient comme la corde la plus grave parmi les sons aigus et comme la plus aigu parmi les plus graves, déterminent 15 cordes pour former la double octave dans le système immuable.

5. Cette échelle est du goût de Ptolémée⁵, qui ajoute que, l'on doit s'en tenir à ce nombre. Il déclare que les tons⁶, égaux en nombre aux espèces de l'octave, comme aux espèces de la quarte et de la quinte⁷, desquelles résulte l'homophone⁸, sont tous compris dans ce nombre de sons⁹; que la mèse est exactement une corde moyenne (μέση) et que les deux extrémités ont pour limites, au grave le proslambanomène, et à l'aigu la nète des hyperboléennes.

Notes

1. Ῥαδιουργία doit signifier, selon nous, le sans-gêne avec lequel les musiciens sortaient des limites consacrées de l'ancien diagramme.

2. Cf. Ptolémée, Harmoniques, l. I, ch. iv.

3. C'est-à-dire de manière que les Sons de ces tétracordes et pentacordes soient consonnants chacun à chacun. Cf. Aristox., El. harm., début du prétendu livre III.

4. Système comprenant deux octaves justes, depuis le proslamanomène jusqu'à la nète hyperboléenne.

5. Cf. Ptolémée, Harmoniques, I. II, ch. iv-v. Meybaum, dans son commentaire, suppose assez gratuitement que ce paragraphe est l'œuvre de celui qui a fait ces extraits; il est moins concluant dans la Préface de son édition de Nicomaque; enfin, dans la préface de son Aristide Quintilien, il donne positivement notre auteur comme à Ptolémée.

6. Il s'agit ici des tons-échelles.

7. Il faut entendre : à la somme de ces espèces.

8. Homophone pris ici dans le sens de consonnant à l'octave (?). Cf. Ptol., Harm., l. II, viii.

9. Le nombre égal à celui des espèces d'octaves. Le texte est mutilé; nous adoptons provisoirement les corrections et la version de Meybaum.

V^e fragment

1. Extrait. — Si quelques-uns ont porté le nombre des sons à 28, il deviendra évident qu'ils se sont écartés de la symphonie de l'Univers, mais se sont conformés à la physique de Pythagore et de Platon¹.

2. En effet, la nature des âmes divines, décomposée au moyen du vingt-septuple auquel elle ajoute l'unité, principe de toutes choses (de même que dans les sons, on emploie symboliquement² le mot proslambanomène) réalise le même nombre, en commençant par les sept termes dont la superposition a permis à Platon de reconnaître la progression triple et cubique et se terminant avec ce nombre³.]

3. Les sons de chacune des sept sphères produisent un certain bruit, la première réalisant le premier son, et à ces sons l'on a donné les noms des voyelles⁴. Ce sont là des choses qualifiées d'inexprimables par elles-mêmes chez les savants, ainsi que tout ce qui est formé, attendu que le son, ici, a la même valeur que l'unité en arithmétique, le point en géométrie, la lettre en grammaire. Si ces choses sont combinées avec des substances matérielles, telles que sont les consonnes, de même que l'âme est unie au corps et l'harmonie aux cordes, elles réalisent des êtres animés⁵, celle-ci des tons et des chants, celle-là des facultés actives⁶ et productrices des choses divines. Voilà pourquoi les Théurges⁷, lorsqu'ils adorent la divinité, l'invoquent symboliquement avec des sifflements ou stridents ou roucoulés⁸, avec des sons inarticulés et sans consonnes.

Notes

1. Aristide Quintilien, Sur la musique, éd. (unique) de Meybaum, p. 136, rapproche les 28 sons des 28 jours du mois lunaire. On fera bien de lire, à titre de rapprochement, tout le livre III de son traité.

2. C'est-à-dire, pour faire allusion à cette adjonction de l'unité.

3. Cf. Platon, Timée, p. 35 A. L'addition des sept premiers nombres donne 28. D'autre part, la progression simple et cubique, c'est le cube de 3, 3³ = 27. Meybaum a remarqué que les sept termes en question sont les nombres 1, 2, 3, 4, 8, 9 et enfin 27, terme « vingt-septuple » énoncé dans le texte. Cf. Théon de Smyrne, Notions de math., etc., p. 150, éd. Boulliau; Th.-H. Martin, Études sur te Timée, note 23, p. 384.

4. Sur les noms des voyelles attribués aux sons et aux planètes, voir Démétrius dit de Phalère, de l'Elocution, § 71. Cf. Mém. de l'Acad. des Inscr., t. XLI, p. 514 et suiv. (Lecture de l'a. J.-J. Barthélemy.)

5. Ou plutôt organisés.

6. Meybaum propose de corriger δραστὶκὰς en φραστικὰς, ce qui nous paraît inutile.

7. Vulgate, Θερινοὶ. Meybaum propose et adopte Τυρρηνοὶ. Nous préférons Θεουργοί, correction donnée par Th. Gale (Rhetores selecti, Oxonii, Notae in Demetr. Phal., p. 235). Cp. Barthélemy, l. c., p. 520.

VI^e fragment

1. Extrait. — Tous ceux qui ont fait usage de la symphonie à sept sons comme étant naturelle, l'empruntaient à cette source, savoir, non pas aux sphères, mais aux sons accordés dans l'univers, les seuls sons que nous appelions, parmi les lettres, sons-voyelles et sons musicaux¹. Mais, comme l'examen est d'une simplicité élémentaire qui ne peut suffire pour expliquer des questions complexes, il faut réaliser la conception de l'Univers par la connexion, analogue à celle des cordes, et par l'ajustement d'une chose avec l'autre².

2. Comment le septénaire a de l'affinité avec le quaternaire et avec l'unité, nous l'avons dit dans notre traité du Septénaire³. Ainsi multiplié par le quaternaire, avec roulement, depuis le premier (terme) jusqu'au dernier, tantôt par accroissement, tantôt par retranchement, il produit pareil nombre, et en effet c'est ce qui a lieu pour les sphères⁴. Or il est évident que, par analogie avec les âmes qui renferment les sphères et les dirigent par un mouvement propre bien réglé⁵ suivant la progression de ces sphères, le son qui leur est inhérent se produisant en surcroît et chacun des autres [sons] étant en défaut quant au nombre par le rythme et par le rang qu'il occupe, il en existe une⁶ à vingt-huit sons conformément à la dénomination qu'elle a reçue des Égyptiens.

3. Pythagore, partant de là, a trouvé que la première division et l'extension de l'âme est déterminée jusqu'à concurrence de ce (nombre). Et en effet celle-ci est triple, ayant reçu l'hypostase (la substance) du Même, de l'Autre et de l'Essence⁷, et, semblablement à l'hypostase, une triple détermination, savoir: le raisonnable, l'irrationnel et le physique, comme aussi l'enharmonique, le diatonique et le chromatique. Et de là ressort clairement une double division dans la psychogonie elle-même, attribuant aux planètes, suivant les sept sons, la constitution, enharmonique par essence, des vingt-sept sons psychiques et physiques, et à la région de la sphère fixe, comme étant la nature du Même et embrassant, dans le mouvement des planètes, aussi bien que la progression cubique suivant l'autre nombre, le nombre parfait 36, lequel a la progression du triangle rectangle dont les deux petits côtés sont comparés à l'hypoténuse⁸, en même temps que réalisant le principe de toutes choses⁹.

4. De là vient le premier quaternaire¹⁰, qui possède la source des consonances sous cette forme : 6, 8, 9, 12, et contient le rapport de l'hypate, de la mèse, de la nète et de la paramèse¹¹. En effet, l'hypate se rapporte au nombre 6, la mèse à 8, la nète à 12 et la paramèse¹² à 9. De plus, le sesquioctave apparaît en premier dans le rapport de 8 à 9. Ce qui est catapycnosé au moyen des diésis¹³, s'élève à un nombre égal à celui des décans et des horonomes¹⁴.

5. Mais, puisqu'il y a huit sphères, comment dit-il que les sons, à ce qu'on prétend, sont au nombre de sept? C'est que la sphère qui se meut toujours dans la même (orbite) donne une émission sonore, invariable et unique, et, comme il n'y a pas d'autre sphère d'une vitesse égale à la sienne, ni qui lui ressemble, elle ne pouvait prendre place dans l'harmonie, attendu que, entre les deux premières (planètes) il y a quelque chose d'analogue, ces deux sphères n'étant ni égales ni tout à fait différentes. Mais, quant aux planètes qui sont sensiblement dissemblables et d'une nature opposée à la sienne¹⁵, on a vu que leur mouvement est dans le même rapport de quantité que celui du Même comparé à celui de l'Autre¹⁶. Voilà pourquoi l'on a laissé sans appellation le son qui vient de cette sphère (fixe).

Notes

1. Φυογγόεις, mot inconnu. On connaît φθογγήεις.

2. Traduit sous toutes réserves.

2. Voir ci-dessus l'Avertissement.

4. Note de Meybaum: « Videtur legendum τετρὰς οὖν πολλαπλασιασθεῖσα. (Nous lisons τετράδι πολλαπλασιασθεῖσα, scil. ἑβδομάς). Hic unus locus est in Nicomacho quem non satis intelligo. Neque enim explicatur quae sit illa τετρὰς, et quem numerum multiplicet. Hoc innuere videtur, septenario multiplicato per 4, consurgere 28, eodem multiplicato per 3 et 1, itidem, 28; per 2 fieri 14, quibus si summae ex 2 in 3 et 4 addantur, consurgere priorem numerum 28. »

5. Vulgate, εὐτάτῳ. Nous lisons εὐτάκτῳ avec Meybaum.

6. Une symphonie.

7. Cp. Platon, Timée, p. 35 B.

8. En effet, 2² x 3² = 6² = 36. L'addition des lignes se traduit par la multiplication des nombres correspondant aux carrés faits sur ces lignes.

9. L'unité.

10. La première tétractys des pythagoriciens.

11 Vulgate, παρανήτη. Correction de Meybaum.

12. Même observation.

13. Diésis pris ici dans le sens de quart de ton. Sur la catapycnose, voir la note 87.

14. Cadrans astrologiques. Cf. Aristide Quintilien, éd. (unique) de Meybaum, p. 152, l. 13.

15. A celle de la sphère fixe.

16. En d'autres termes, la sphère fixe est au Même ce que les sphères planétaires sont à l'Autre. Cp. Platon, Timée, p. 36 C.

VIl^e Fragment

1. Extrait. — Les sons dont s'occupent ceux qui se livrent à la facture des instruments, sont les suivants :

Proslambanomène.................................................

Hypate des hypates...............................................

Parhypate des hypates..........................................

Enharmonique des hypates...................................

Chromatique des hypates......................................

Diatonique des hypates.........................................

Hypate des moyennes...........................................

Parhypate des moyennes......................................

Enharmonique des moyennes..............................

Chromatique des moyennes.................................

Diatonique des moyennes.....................................

Mèse........................................................................

Trite des conjointes.................................................

Paranète enharmonique des conjointes..............

Chromatique des conjointes..................................

Diatonique des conjointes......................................

Nète des conjointes................................................

Paramèse................................................................

Trite des disjointes.................................................

Enharmonique des disjointes................................

Chromatique des disjointes...................................

Diatonique des disjointes......................................

Nète des disjointes.................................................

Trite des hyperboléennes......................................

Enharmonique des hyperboléennes.....................

Chromatique des hyperboléennes........................

Diatonique des hyperboléennes...........................

Nète des hyperboléennes......................................

2. De même donc qu'ici nous avons des tétracordes dans les trois genres, savoir, les tétracordes des hypates, ceux des moyennes, ceux des conjointes, ceux des disjointes et ceux des hyperboléennes, de même il faut croire que chaque essence sphérique et divine a reçu ce qui a dans le Tout comme un rapport de principe, eu égard à l'harmonie et à la constitution du monde, puis comme un rapport de moyenne, et enfin comme un rapport de fin, puis l'effet d'une coopération conjonctive, puis celui d'une coopération séparative¹; — que la Providence, usant pleinement de tous ces éléments, produit le nombre divin, fixe et inébranlable et le Tout, en accord mélodique avec lui-même; qu'elle relie ensemble toute essence dominatrice et subalterne suivant cette proportion et dans cet ordre.

3. Ainsi donc le premier quaternaire², qui est aussi la racine de ces tétracordes, est, dans un certain sens, apte à fournir toutes les divisions par genres³, réalisant, comme nous l'avons dit⁴, le nombre 36 qui est propre à la sphère fixe, au moyen de l'addition de l'unité⁵.

4. Platon, voulant montrer cette clef des êtres, au livre XIII des Lois, s'exprime ainsi, après avoir énuméré jusqu'à la dernière des sciences qu'il avait passées en revue:

« La Nature a encore attribué aux hommes un usage consonnant et bien proportionné ...⁶ »

Notes

1. On voit que les cinq articles correspondent aux cinq tétracordes.

2. En grec, τετρακτύς.

3 .En d'autres termes, les variétés de genre.

4. Voir ci-dessus le VI^e fragment, § 4.

5. 6 + 8 +9 + 12 =37 =36 + 1.

5. Platon, Lois, XIII (Epinomis), p. 991 B.