|
Muet jusqu'à l'âge de sept ans, et sourd. Professeur au collège de France en 1686. On le reconnaît comme le fondateur de l'acoustique en tant que science particulière. Avec ses élèves, il détermine le nombre exact des vibrations sonores en comparant les différences de battements émis par les tuyaux d'orgue.
Application des sons harmoniques à la composition des jeux d'orgues. Tiré des Mémoires de 1702 de l'Académie royale des sciences. Par Mr. Sauveur.
Principes d'acoustique et de musique, ou système général des intervalles des sons, et de son application à tous les systèmes et à tous les instrumens de musique. Inséré dans les mémoires de 1701 de l'Académie Royale des Sciences. Par Mr. Sauveur.
Éditions Modernes
Principes. Minkoff reprint, Genève 1973 [68 p., ill., 23 cm]
RUDOLPH RASCH (éd.),
Sauveur Joseph. Collected Writings on Musical Acoustics: Paris, 1700-1713. Diapason Press, Utrecht 1984
SEMMENS RICHARD,
Joseph Sauveur’s Treatise of the Theory of Music. A Study, Diplomatic Transcription and Annotated Translation. Dans «Studies in Music from the University of Western Ontario» (11) 1987
Bibliographie
HANDSCHIN JACQUES,
Der Toncharakter. Zürich 1948
MAXHAM ROBERT EUGENE,
The Contributions of Joseph Sauveur (1653-1716) to Acoustics (thèse). University of Rochester 1976 [2 v., xi-360 p., RILM 76:4426dd]
SCHERCHEN HERMANN (1891-1966),
Vom Wesen des Musik. Zürich, Mondial Verlag 1946; Winterthur et Regensburg 1947; The nature of music, traduit par William Mann, Londres, D. Dobson 1950; Chicago, H. Regnery 1950; St. Clair Shores, Mich., Scholary Press 1972
SOUBERBIELLE LÉON,
Le Plein-jeu de l’orgue français à l’époque classique : 1660-1740. Montoire-sur-Loir, 1977
JEAN-MARC WARSZAWSKI,
Dictionnaire des écrits sur la musique (2 v.). Berne, Francfort, New York, Peter Lang 2004 [2 vol., 2324 p., ISBN 3-906766-83-7] t2, p. 1690
Ainsi le son qui monte, passe par les intervalles d'une première, d'une seconde, d'une troisième etc. Lorsqu'il fait 2, 4, 8, 16 etc. vibrations contre le premier, et ce son passe par des semblables octaves en descendant lorsqu'il ne fait que 1/2, 1/4, 1/6... des vibrations du premier son. (Système général, 1701)
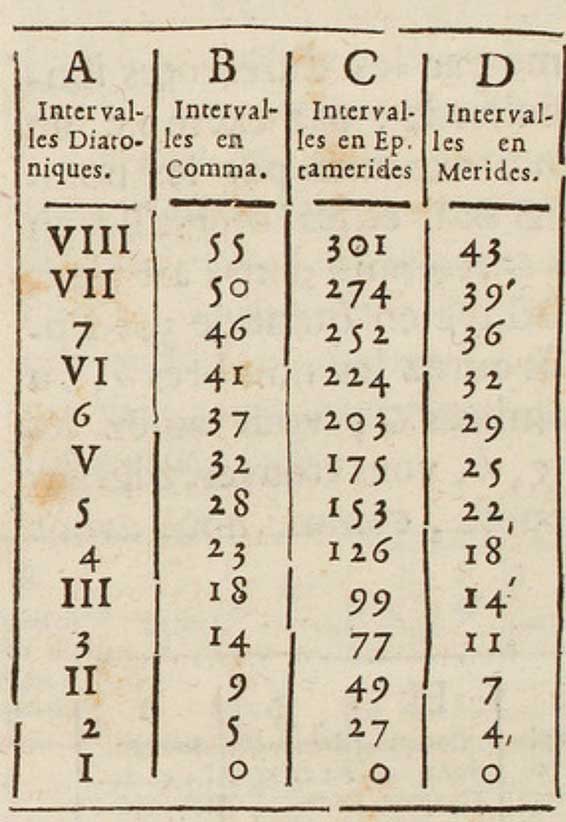
Il divise l'octave en 43 parties égales qu'il nomme mérides, puis chaque méride en 7 eptamérides. C'est à dire que l'octave est divisée en 301 parties. Il peut dès lors exprimer tous les intervalles de tous les systèmes en mérides et eptamérides. Il fixe un son de référence de 100 vibrations par seconde, contre les variations constantes du ton (ton de l'Opéra, de la Chapelle Royales etc.) Je pris en 1696 le parti de trouver une mesure commune à tous les intervalles, capables de les mesurer dans leurs différences les moins sensibles, de donner des noms et des caractères à tous ces sons, qui fussent tels qu'on pût prendre ceux qui seraient nécessaires à la musique ordinaire et qui renfermassent d'une manière simple et aisée toutes les propriétés qui regardent cet art, sans néanmoins avoir dessein d'exclure les notes auxquelles les musiciens sont accoutumés depuis si longtemps.(Système général, p. 300)
Application des sons harmoniques à la composition des jeux d'orgues (1702)
De tout ce que nous avons dit des orgues, nous en pouvons tirer les conséquences suivantes.1- La composition des jeux d'orgues est harmonique, comme il parait for les nombres que nous avons mis dans la table des jeux d'orgue. 2- Le mélange des jeux est harmonique, et si l'on s'en écarte, c'est une espèce de dissonance dans les sons harmoniques, qui a du rapport avec les dissonances qu'on emploie dans la musique.3- L'orgue ne fait qu'imiter par le mêlange de ses jeux, l'harmonique que la nature observe dans les corps sonores, qu'on appelle harmonieux, car on y distingue les sons harmoniques 1, 2, 3, 4, 5, 6 comme dans les cloches et la nuit dans les longues cordes du clavecin. Cette harmonie paraît surtout dans les cornets. 4- L'orgue sert à nous faire distinguer le son le plus grave et le son le plus aigu, l'étendue de tous les sons et enfin ceux que l'on distingue le plus nettement. Jusqu'à l'intervalle diatonique, 85e ou 4096e son harmonique.
| |
Anciens noms |
nouveaux noms |
eptamérides |
mérides |
| |
sol # |
ba b8 bu |
1960 1890 1820 |
1960 1890 1820 |
| V |
sol |
bo |
1750 |
25 |
| 5 |
sol b |
bi b e be |
1680 1610 1540 |
24 23 22 |
| IV |
fa # |
fa f8 fu |
1470 1400 1330 |
21 20 19 |
| 4 |
fa |
so |
1260 |
18 |
| |
|
si g1 sé g e sé g e |
1150 1120 1050 |
17 16 15 |
| III |
mi |
ga |
90 |
14 |
| 3 |
mi b |
g8 gu go |
910 840 770 |
13 12 11 |
| |
ré # |
ri re ré |
700 630 560 |
10 9 8 |
| II |
ré |
ra |
790 |
7 |
| 2 |
ré b |
r8 ru ro |
420 350 280 |
6 5 4 |
| |
ut # |
ri re ré |
210 140 70 |
3 2 1 |
| |
ut fond. |
pa |
0 |
0 |
| |
si # |
p8 da pu d8 otb |
2940 2870 2800 |
42 41 40 |
| VII |
si |
do |
2370 |
39 |
| 7 |
si b |
de |
2660 2590 2520 |
38 37 36 |
| |
la # |
la l8 lu |
2450 2380 2310 |
35 34 33 |
| VI |
la |
lo |
2240 |
32 |
| 6 |
la |
li le le |
2170 2100 2030 |
31 30 29 |
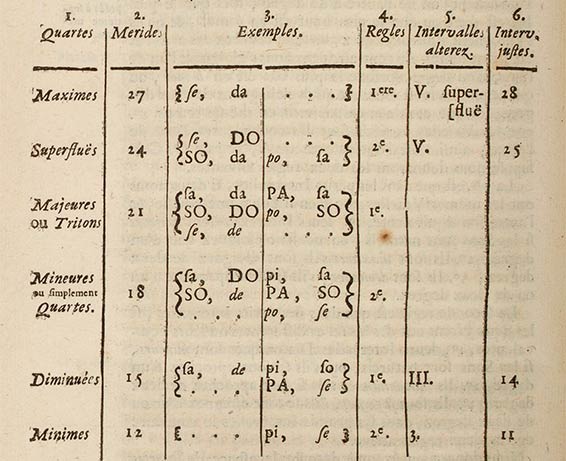
Système général (1701)
Préface
Personne n'a fait jusqu'ici, de la musique une science supérieure, qui détachée, lui convienne particulièrement. J'ai donc cru qu'il y avait une science supérieure à la musique, que j'ai appelé acoustique, qui a pour objet la son en général, au lieu que la musique a pour objet le son en tant qu'il est agréable à l'ouïe.
Un son de référence
Les musiciens prennent pour son fondamental le C sol, ut, ton de la chapelle et de l'Opéra. Milieu du clavecin. [Ce son n'est pas assez déterminé]. Nous prenons pour son fondamental le son fixe, qui fait cent vibrations dans une seconde de temps dont j'ai déjà parlé ci-dessus
Mérides et eptamérides
C'est avec ces parties que nous exprimerons son seulement les intervalles ordinaires de musique, mais encore tous les intervalles qu'on peut imaginer dans l'acoustique. T, Ton majeur, 7 mérides et 2 eptamérides. 7'' ; t, Ton mineur, 7 mérides moins 3 eptamérides. 7'''. S, Semi-ton majeur, 4 mérides.
| Échelle diatonique |
Intervalles comma |
Eptamérides |
Mérides |
| VIII |
55 |
301 |
43 |
| VII |
50 |
274 |
29 |
| 7 |
46 |
252 |
36 |
| VI |
41 |
144 |
32 |
| 6 |
37 |
203 |
29 |
| V |
32 |
175 |
25 |
| IV ou 5 |
28 |
153 |
22 |
| 4 |
23 |
126 |
18 |
| III |
18 |
99 |
14 |
| 3 |
14 |
77 |
11 |
| II |
9 |
49 |
7 |
| 2 |
5 |
27 |
4 |
| I |
0 |
0 |
|
Localisation des livres imprimés
Application des sons harmoniques
F : Paris, Bibliothèque de France, département de la musique - Paris, Bibliothèque nationale - Troyes, Bibliothèque municipale - I : Bologna, Biblioteca del Conservatorio (Liceo Musicale ; oggi civico Museo Bibliografico Musicale) - US : Cambridge, Mass., Eda Kuhn Loeb - Music Library, Harvard University
Principes d'acoustique et de musique
B : Bruxelles, Bibliothèque Royale - F : Paris, Bibliothèque de l’Arsenal - Paris, Bibliothèque de France, département de la musique - Paris, Bibliothèque nationale - Troyes, Bibliothèque municipale - GB : Glasgow, Euing Musical library
|
